Structure
General theory
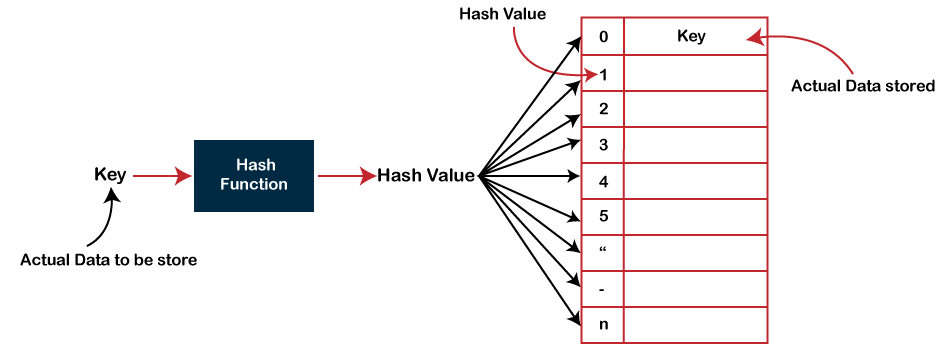
Plenty of modern programming languages include hash tables as the base data type. On the outside, a hash table looks like a regular array that is indexed with any data type (for example, string) rather than with an integer number. Hash index in PostgreSQL is structured in a similar way. How does this work?
As a rule, data types have very large ranges of permissible values: how many different strings can we potentially envisage in a column of type “text”? At the same time, how many different values are actually stored in a text column of some table? Usually, not so many of them.
The idea of hashing is to associate a small number (from 0 to N−1, N values in total) with a value of any data type. Association like this is called a hash function. The number obtained can be used as an index of a regular array where references to table rows (TIDs) will be stored. Elements of this array are called hash table buckets – one bucket can store several TIDs if the same indexed value appears in different rows.
The more uniformly a hash function distributes source values by buckets, the better it is. But even a good hash function will sometimes produce equal results for different source values – this is called a collision. So, one bucket can store TIDs corresponding to different keys, and therefore, TIDs obtained from the index need to be rechecked.
Just for example: what hash function for strings can we think of? Let the number of buckets be 256. Then for example of a bucket number, we can take the code of the first character (assuming a single-byte character encoding). Is this a good hash function? Evidently, not: if all strings start with the same character, all of them will get into one bucket, so the uniformity is out of the question, all the values will need to be rechecked, and hashing will not make any sense. What if we sum up codes of all characters modulo 256? This will be much better, but far from being ideal. If you are interested in the internals of such a hash function in PostgreSQL, look into the definition of hash_any() in hashfunc.c.
Index structure
Let’s return to hash index. For a value of some data type (an index key), our task is to quickly find the matching TID.
When inserting into the index, let’s compute the hash function for the key. Hash functions in PostgreSQL always return the “integer” type, which is in range of 232 ≈ 4 billion values. The number of buckets initially equals two and dynamically increases to adjust to the data size. The bucket number can be computed from the hash code using the bit arithmetic. And this is the bucket where we will put our TID.
But this is insufficient since TIDs matching different keys can be put into the same bucket. What shall we do? It is possible to store the source value of the key in a bucket, in addition to the TID, but this would considerably increase the index size. To save space, instead of a key, the bucket stores the hash code of the key.
When searching through the index, we compute the hash function for the key and get the bucket number. Now it remains to go through the contents of the bucket and return only matching TIDs with appropriate hash codes. This is done efficiently since stored “hash code – TID” pairs are ordered.
However, two different keys may happen not only to get into one bucket, but also to have the same four-byte hash codes – no one has done away with the collision. Therefore, the access method asks the general indexing engine to verify each TID by rechecking the condition in the table row (the engine can do this along with the visibility check).
Mapping data structures to pages
If we look at an index as viewed by the buffer cache manager rather than from the perspective of query planning and execution, it turns out that all information and all index rows must be packed into pages. Such index pages are stored in the buffer cache and evicted from there exactly the same way as table pages.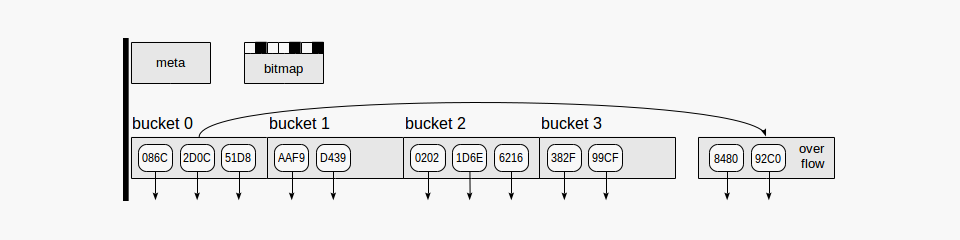
Hash index, as shown in the figure, uses four kinds of pages (gray rectangles):
- Meta page – page number zero, which contains information on what is inside the index.
- Bucket pages – main pages of the index, which store data as “hash code – TID” pairs.
- Overflow pages – structured the same way as bucket pages and used when one page is insufficient for a bucket.
- Bitmap pages – which keep track of overflow pages that are currently clear and can be reused for other buckets.
Down arrows starting at index page elements represent TIDs, that is, references to table rows.
Each time the index increases, PostgreSQL instantaneously creates twice as many buckets (and therefore, pages) as were last created. To avoid allocation of this potentially large number of pages at once, version 10 made the size increase more smoothly. As for overflow pages, they are allocated just as the need arises and are tracked in bitmap pages, which are also allocated as the need arises.
Note that hash index cannot decrease in size. If we delete some of indexed rows, pages once allocated would not be returned to the operating system, but will only be reused for new data after VACUUMING. The only option to decrease the index size is to rebuild it from scratch using REINDEX or VACUUM FULL command.
Example
Let’s see how hash index is created. To avoid devising our own tables, from now on we will use the demo database of air transportation, and this time we will consider the flights table.
demo=# create index on flights using hash(flight_no);
WARNING: hash indexes are not WAL-logged and their use is discouraged
CREATE INDEX
demo=# explain (costs off) select * from flights where flight_no = 'PG0001';
QUERY PLAN
----------------------------------------------------
Bitmap Heap Scan on flights
Recheck Cond: (flight_no = 'PG0001'::bpchar)
-> Bitmap Index Scan on flights_flight_no_idx
Index Cond: (flight_no = 'PG0001'::bpchar)
(4 rows)
What’s inconvenient about the current implementation of hash index is that operations with the index are not recorded in the write-ahead log (of which PostgreSQL warns when the index is created). In consequence, hash indexes cannot be recovered after failure and do not participate in replications. Besides, hash index is far below “B-tree” in versatility, and its efficiency is also questionable. So it is now impractical to use such indexes.
However, this will change as early as this autumn (2017) once version 10 of PostgreSQL is released. In this version, hash index finally got support for the write-ahead log; additionally memory allocation was optimized and concurrent work made more efficient.
That’s true. Since PostgreSQL 10 hash indexes have got full support and can be used without restrictions. The warning is not displayed anymore.
Hashing semantics
But why ever did hash index survive nearly from the very birth of PostgreSQL to 9.6 being unusable? The thing is that DBMS make extensive use of the hashing algorithm (specifically, for hash joins and groupings), and the system must be aware of which hash function to apply to which data types. But this correspondence is not static, and it cannot be set once and for all since PostgreSQL permits new data types to be added on the fly. And this is an access method by hash, where this correspondence is stored, represented as an association of auxiliary functions with operator families.
demo=# select opf.opfname as opfamily_name,
amproc.amproc::regproc AS opfamily_procedure
from pg_am am,
pg_opfamily opf,
pg_amproc amproc
where opf.opfmethod = am.oid
and amproc.amprocfamily = opf.oid
and am.amname = 'hash'
order by opfamily_name,
opfamily_procedure;
opfamily_name | opfamily_procedure
--------------------+--------------------
abstime_ops | hashint4
aclitem_ops | hash_aclitem
array_ops | hash_array
bool_ops | hashchar
...
Although these functions are not documented, they can be used to compute the hash code for a value of the appropriate data type. For example, “hashtext” function if used for the “text_ops” operator family:
demo=# select hashtext('one');
hashtext
-----------
127722028
(1 row)
demo=# select hashtext('two');
hashtext
-----------
345620034
(1 row)
Properties
Let’s look at the properties of hash index, where this access method provides the system with information about itself. We provided queries last time. Now we won’t go beyond the results:
name | pg_indexam_has_property
---------------+-------------------------
can_order | f
can_unique | f
can_multi_col | f
can_exclude | t
name | pg_index_has_property
---------------+-----------------------
clusterable | f
index_scan | t
bitmap_scan | t
backward_scan | t
name | pg_index_column_has_property
--------------------+------------------------------
asc | f
desc | f
nulls_first | f
nulls_last | f
orderable | f
distance_orderable | f
returnable | f
search_array | f
search_nulls | f
A hash function does not retain the order relation: if the value of a hash function for one key is smaller than for the other key, it is impossible to make any conclusions how the keys themselves are ordered. Therefore, in general hash index can support the only operation “equals“:
demo=# select opf.opfname AS opfamily_name,
amop.amopopr::regoperator AS opfamily_operator
from pg_am am,
pg_opfamily opf,
pg_amop amop
where opf.opfmethod = am.oid
and amop.amopfamily = opf.oid
and am.amname = 'hash'
order by opfamily_name,
opfamily_operator;
opfamily_name | opfamily_operator
---------------+----------------------
abstime_ops | =(abstime,abstime)
aclitem_ops | =(aclitem,aclitem)
array_ops | =(anyarray,anyarray)
bool_ops | =(boolean,boolean)
...
Consequently, hash index cannot return ordered data (“can_order”, “orderable”). Hash index does not manipulate NULLs for the same reason: the “equals” operation does not make sense for NULL (“search_nulls”).
Since hash index does not store keys (but only their hash codes), it cannot be used for index-only access (“returnable”).
This access method does not support multi-column indexes (“can_multi_col”) either.
Internals
Starting with version 10, it will be possible to look into hash index internals through the “pageinspect” extension. This is what it will look like:
demo=# create extension pageinspect;
The meta page (we get the number of rows in the index and maximal used bucket number):
demo=# select hash_page_type(get_raw_page('flights_flight_no_idx',0));
hash_page_type
----------------
metapage
(1 row)
demo=# select ntuples, maxbucket
from hash_metapage_info(get_raw_page('flights_flight_no_idx',0));
ntuples | maxbucket
---------+-----------
33121 | 127
(1 row)
A bucket page (we get the number of live tuples and dead tuples, that is, those that can be vacuumed):
demo=# select hash_page_type(get_raw_page('flights_flight_no_idx',1));
hash_page_type
----------------
bucket
(1 row)
demo=# select live_items, dead_items
from hash_page_stats(get_raw_page('flights_flight_no_idx',1));
live_items | dead_items
------------+------------
407 | 0
(1 row)
And so on. But it is hardly possible to figure out the meaning of all available fields without examining the source code. If you wish to do so, you should start with README.
reference: https://postgrespro.com/blog/pgsql/4161321